Beim Gamma handelt es sich um eine beliebte Kennzahl für die Optionshändler. Diese Kennzahl drückt immer aus, wie sich das Delta der Option in Abhängigkeit zum Kurs des Basiswerts verändert. Dabei finden andere Faktoren, die die Preise der Optionen ebenfalls beeinflussen, keinerlei Berücksichtigung. Folglich ist das Gamma eine der Kennzahlen, die sich immer direkt auf eine andere Kennzahl beziehen. Im folgenden Beitrag geht es um die Definition, die Berechnung und die Anwendung des Gammas.
Gamma einer Option: Was ist das?
- Das Gamma ist ein Optionsgrieche und somit eine Sensitivitätskennzahl.
- Es bezeichnet die Krümmung der Preiskurve.
- Gamma gilt als Kennzahl zur Absicherung eines Depots.
Definition vom Gamma
Beim Gamma handelt es sich aus der mathematischen Perspektive um eine Krümmung der Preiskurve einer Option. Wenn das Gamma niedrig ist, kann das Delta die Preisänderung besser beschreiben. Bei einem großen Gamma ist das Gegenteil der Fall. Die Kennzahl beschreibt somit immer nur, wie sich das Delta verändert, wenn der Kurs des Basiswerts um eine definierte Preiseinheit steigt oder fällt.
Häufig kommt das Gamma als Kennzahl bei der Absicherung von Depots zum Einsatz. Viele Optionshändler versuchen ihre Portfolios mit einem neutralen Gamma zu strukturieren. Dafür werden Optionen aufgenommen, die das Gamma kompensieren. Denn ein Portfolio bleibt nur für einen kurzen Zeitraum mit einem neutralen Delta versehen, da sich diese Kennzahl schnell ändert. Wenn das Portfolio jedoch mit einem neutralen Gamma strukturiert ist, bleibt der neutrale Delta-Wert für einen längeren Zeitraum bestehen.
Mein Tipp: Jetzt über zahlreiche Optionen zu den besten Konditionen bei IG traden:
Berechnung vom Gamma
Die Berechnung der Kennzahl Gamma hängt vom Delta der Option ab. Denn das Gamma zeigt an, wie stark sich das Delta verändert, wenn der Kurs eines Basiswerts fällt oder steigt. Folglich handelt es sich bei der Berechnung um die zweite Ableitung des Preises einer Option. Ganz gleich, ob es sich um die Berechnung für Call oder Put Optionen handelt – das Gamma einer Option hat einen Wert, der größer als Null ist.
Die Berechnung erfolgt typisch für die Optionsgriechen mit der Black-Scholes-Formel. Da die individuelle Berechnung sehr komplex ist, übernehmen die Broker diese Berechnung mit einer speziellen Software. Die Preise der Option werden dann durch Angebot und Nachfrage bestimmt.
Das Gamma von Call und Put Optionen hat den identischen Wert, wenn die anderen Rahmenbedingungen gleich sind. Dazu gehören der gleiche zugrunde liegende Basiswert, der identische Strike und die Laufzeit der Option. Folglich spielt es bei der Berechnung des Gammas nur eine untergeordnete Rolle, ob es sich um eine Call oder Put Option handelt. Ohne die Berücksichtigung anderer Einflussfaktoren wirkt sich das Gamma direkt auf das Delta einer Option aus. Daraus resultieren mittelbare Auswirkungen auf die Preise der Option.
Beispielsweise kommt eine Berechnung des Gammas zu den folgenden Auswirkungen:
- Kurs des Basiswerts steigt um 1: altes Delta + Gamma-Wert = steigender Preis der Option
- Kurs des Basiswerts sinkt um 1: altes Delta – Gamma Wert = fallender Preis der Option
Put Option:
- Kurs des Basiswerts steigt um 1: altes Delta – Gamma Wert: fallender Preis der Option
- Kurs des Basiswerts sinkt um 1: altes Delta + Gamma Wert: steigender Preis der Option
Anwendung vom Gamma
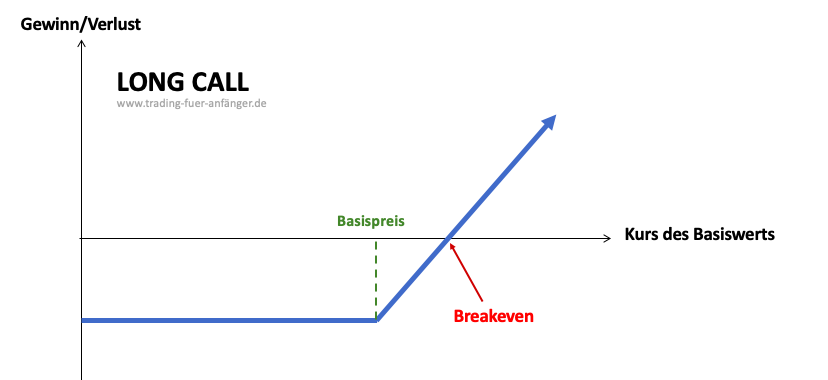
Das Gamma lässt sich auf Put und Call Optionen gleichermaßen anwenden. Wenn ein Long Call ein Gamma von 0,2 und ein Delta von 0,5 hat, gibt es die folgenden Auswirkungen:
- Kurs des Basiswerts steigt um eine Einheit
- Neues Delta der Option beträgt 0,7
- Kurs des Basiswerts fällt um eine Einheit
- Neues Delta der Option beträgt 0,2
Tipp: Jetzt über 1.000 verschiedene Optionen zu besten Konditionen traden:
- In Deutschland Reguliert (BaFin)
- Sehr großes Angebot an Assets
- Viele Finanzprodukte
- Gutes Weiterbildungsangebot
- Schnelle Marktausführung
- Streng reguliert
- 24/7 Support
- Garantierte Stops möglich
- Nutzerfreundliche Plattform
- Große Auswahl an CFDs und echten Aktien
Interpretation des Gamma
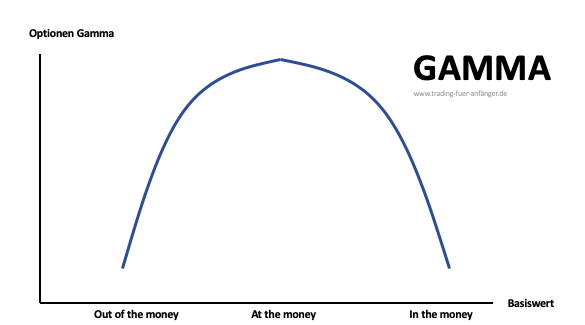
Die Kennzahl Gamma ist eine variable Kennzahl. Diese wird wie die meisten anderen Optionsgriechen durch eine Veränderung des Basiswerts beeinflusst. Bei einer Option, die sich at the money befindet, ist das Gamma besonders hoch. Bereits kleine Bewegungen beim Kurs des Basiswerts führen zu stärkeren Auswirkungen auf das Delta der Option.
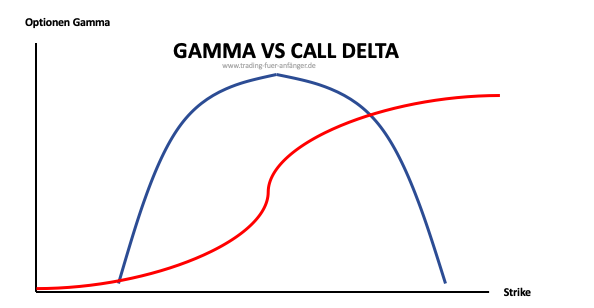
Wenn eine Option ein hohes Gamma hat, ist bei einer Call Option auch der Delta-Wert höher, sofern der Kurs des Basiswerts steigt. Bei einer Put Option ist die Entwicklung die Gleiche, wenn der Basiswert fällt. Folglich fungiert diese Entwicklung mit einer Art Hebelwirkung auf den Preis einer Option. Wenn Optionen relativ weit out of the money notieren oder in the money liegen, beträgt die Kennzahl Gamma gegen null. Die Verluste halten sich dann in Grenzen. Das Gamma wird immer kleiner.
Zugleich beeinflusst die Laufzeit der Option die Interpretation des Gammas. Wenn die restliche Laufzeit einer Option gering ist, steigt das Gamma an. Kleine Veränderungen des Kurs des Basiswerts können sich dann schon gravierend auf den Preis einer Option auswirken. Das Gamma ist somit besonders hochwertig, wenn die Option in den nächsten Tagen fällig ist oder sich besonders nah am Geld (at the money) befindet. Daraus resultiert das sogenannte Gamma-Risiko, das Optionshändler unbedingt berücksichtigen sollten. Die Kennzahl Delta weist eine höhere Sensitivität auf, wenn das Verfallsdatum der Option näher rückt. Dies lässt sich auf das Gamma übertragen.
Bei der Kennzahl Gamma handelt es sich um eine Sensitivitätskennzahl, die in Abhängigkeit vom Kurs des Basiswerts steht. Sofern sich dieser um eine Einheit verändert, variiert auch das Gamma. Folglich hat das Gamma keine Konstanz. Es findet immer wieder eine neue Bildung statt, sodass Optionshändler unbedingt das aktuelle Gamma berechnen und berücksichtigen müssen.
Gamma und die anderen Optionsgriechen
Beim Gamma handelt es sich um einen sogenannten Optionsgriechen. Diese Sensitivitätskennzahlen geben die Auswirkung von Veränderungen beim Kurs des Basiswerts auf den Optionspreis an. Dabei beziehen sich die Kennzahlen lediglich auf einzelne Einflussfaktoren.

Das Gamma beschreibt die Veränderungsrate vom Delta, welches wiederum die Preisänderung einer Option angibt, wenn der Kurs des Basiswerts steigt oder fällt. Die vier folgenden Optionsgriechen sind in der Praxis äußerst relevant und sollten von Tradern berücksichtigt werden:
- Delta: Auswirkungen einer Kursänderung beim Basiswert auf den Preis einer Option
- Gamma: Auswirkungen einer Kursänderung beim Basiswert auf das Delta
- Theta: Auswirkungen vom Zeitverlauf auf den Preis einer Option
- Vega: Auswirkungen der impliziten Volatilität auf den Preis einer Option
Fazit: Gamma stellt die Krümmung der Preiskurve einer Option dar
Das Gamma einer Option gibt den Händlern ein Gefühl, wie stark sich die Kennzahl in Abhängigkeit zum Kurs des Basiswerts verändert. Dabei wird immer die Veränderung des Aktienkurses um eine Einheit angenommen. Rechnerisch stellt das Gamma die Krümmung der Preiskurve einer Option dar. Grundsätzlich lassen sich das Gamma von einer Put oder einer Call Option auf die gleiche Art und Weise berechnen. Sowohl die Moneyness als auch die Restlaufzeit beeinflussen die Höhe eines Gammas. Wenn sich Optionen in the money befinden, ist der Gamma-Wert besonders hoch. Der Wert dieser Kennzahl sinkt jedoch, wenn die Optionen weit out of the money oder tief in the money notieren.
Mein Tipp: Jetzt über zahlreiche Optionen zu den besten Konditionen bei IG traden:
Meist gestellte Fragen:
Was sagt das Gamma bei Optionen aus?
Das Gamma gibt Aufschluss darüber, wie stark sich das Delta einer Option ändert, wenn der Kurs des zugrundeliegenden Basiswerts um 1 USD steigt oder sinkt. Insofern kann das Gamma auch als „Delta des Delta“ bezeichnet werden.
Wo finde ich das Gamma einer Option?
Das Gamma finden Sie bei Optionen für gewöhnlich in der Handelsplattform ihres Brokers, wenn Sie die jeweilige Option ausgewählt haben. Viele Handelsplattformen haben einen entsprechend gekennzeichneten Bereich, in dem sämtliche Optionsgriechen übersichtlich angezeigt werden.
Was passiert bei einem Gamma Squeeze?
Bei einem Gamma Squeeze steigt der Kurs des zugrundeliegenden Basiswerts stark an, sodass Stillhalter, die ungedeckte Call-Optionen verkauft haben, in Bedrängnis geraten und sich mit dem Basiswert eindecken, um ihre Lieferverpflichtungen zu erfüllen, bevor der Kurs noch weiter ansteigt. Dies treibt den Kurs des Basiswerts noch weiter in die Höhe, womit auch das Delta der darauf gehandelten Optionen immer stärker ansteigt. Die Stärke dieses Anstiegs lässt sich mit dem Gamma nachverfolgen, weshalb man hier von einem „Gamma Squeeze“ spricht.
Können Optionen auch ein negatives Gamma haben?
Ja, das Gamma von Optionen kann auch negativ sein. Dies ist bei verkauften Optionen der Fall. Das Gamma von gekauften Optionen hingegen ist immer positiv.