Das Delta ist eine wichtige Kennzahl für alle Optionshändler. Diese ist der zentrale Optionsgrieche, welcher die Sensitivität eines bestimmten Einflussfaktoren angibt. Das Delta verweist darauf, wie viel sich der Preis einer Option ändert, wenn der Kurs eines Basiswerts um eine Geldeinheit steigt oder fällt. Zugleich weist das Gamma eine starke Relation zum Delta der Option auf. Im folgenden Beitrag gibt es alles Wissenswerte über Definition, Interpretation, Anwendung sowie Berechnung der Kennzahl Delta.
Gamma einer Option: Was ist das?
- Das Delta ist ein Optionsgrieche und somit eine Sensitivitätskennzahl.
- Es zeigt das Verhältnis zwischen der Preis- und Kursveränderung einer Option im Vergleich zum Basiswert.
- Das Delta kann Werte zwischen 0 und 1 annehmen.
Definition vom Delta
Das Delta ist die bekannteste Kennzahl für den Optionshandel. Mit dem Delta kann man angeben, inwieweit sich die Veränderung des Preises einer Option in Relation zu einem veränderten Kurs des Basiswerts verhält. Zugleich lässt sich dann mit dem Delta die Position errechnen, die durch einen Optionskontrakt abgebildet wird. Dabei ist jedoch die erste Definition besonders gebräuchlich. Mit dem Delta schaut man sich die Wertveränderung einer Option an, wenn sich der Kurs des Basiswerts in eine Richtung verändert. Standardmäßig sinkt oder steigt der Preis der Option, wenn sich der Kurs des Basiswerts verändert. Das Delta gibt dann an, wie stark dieser Anstieg oder das Absinken erfolgt, wenn sich alle anderen Einflussfaktoren für den Optionspreis nicht verändern.
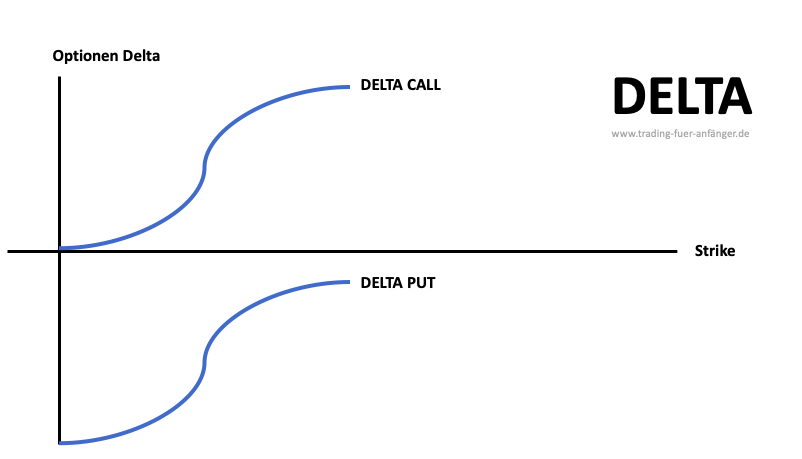
Das Delta einer Option wird mit Zahlen zwischen -1 und +1 angegeben. Bei Call Optionen ist ein positives Delta möglich, bei Put Optionen gibt es ein negatives Delta. Der Wert dieser Kennzahl gilt als variabel, da er sich kontinuierlich verändert. Während der Laufzeit einer Option kann man mit dem Delta die möglichen Veränderungen berechnen. Wenn sich eine Option in the money befindet, ist das Delta deutlich höher. Je weiter die Option jedoch aus dem Geld liegt, desto niedriger ist der Wert des Deltas.
Mein Tipp: Jetzt über zahlreiche Optionen zu den besten Konditionen bei IG traden:
Interpretation vom Delta
Die Kennzahl Delta findet dann Verwendung, wenn es um eine Beurteilung der Reaktion des Preises einer Option geht. Hier wird der Preis einer Option mit dem Kurs eines Basiswerts in Relation gesetzt. Sofern sich der Kurs des Basiswerts um eine Geldeinheit – häufig 1 Euro oder 1 US-Dollar – verändert, gibt das Delta diese Änderungsrate an. Wichtig für die Interpretation des Deltas ist die Moneyness einer Option sowie die Laufzeit. Denn der Abstand zum Stichtag für die Ausübung kann das Delta grundlegend beeinflussen.
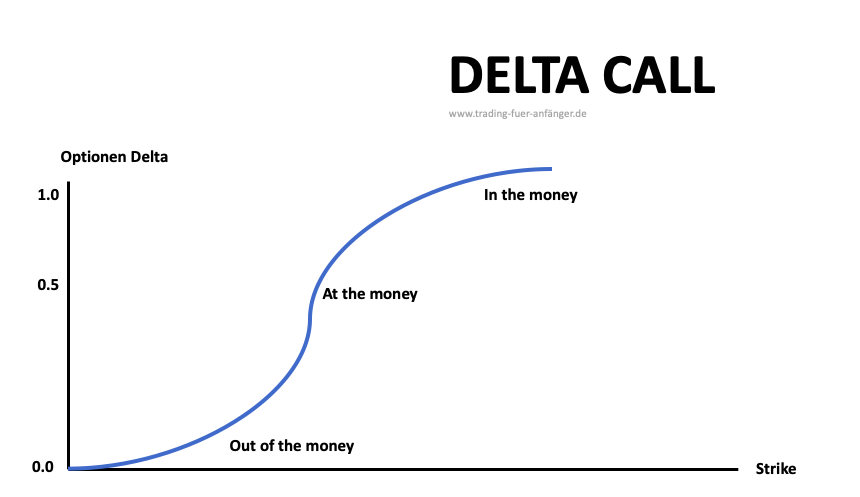
Wenn sich eine Call Option im Geld befindet, ist ein Delta von 1 das Ziel. Je tiefer die Option in the money liegt und je näher der Verfallstag kommt, desto näher kommt das Delta dem Wert von 1. Bei einer Option, die at the money notiert, gibt es ein Delta von 0,5. Sofern sich die Option out of the money befindet, wird das Delta wieder geringer. Bei einer Put Option ist das Gegenteil der Fall und die Interpretation kann spiegelbildlich dargestellt werden. Long Put Optionen steigen grundsätzlich, wenn der Kurs des Basiswerts sinkt. Daraus resultieren negative Deltas bei einer Put Option. Bei einem Put läuft das Delta Richtung -1, wenn dieser weiter in the money notiert. At the money ist das Delta bei -0,5. Das Delta einer Put Option geht gegen 0, wenn sich diese weit out of the money befindet.
Bei Call und Put Optionen bedeutet ein Delta von O, dass keine Korrelation zwischen dem Preis der Option und dem Kurs des Basiswerts besteht. Dann ist der Preis einer Option von der Entwicklung des Kurses des Basiswerts abgekoppelt. Ein Zusammenhang besteht nicht.
Anwendung vom Delta
Das Delta lässt sich einsetzen, wenn Optionshändler den Zusammenhang zwischen Kurs des Basiswerts und Preis der Option analysieren wollen. Zudem ist das Delta ein Indikator, um die Chance zu analysieren, ob eine Option bei Fälligkeit in the money liegt oder eben nicht. Bei einem Delta von 0,5 würde die Chance bei 50 % liegen, dass die Option am Stichtag in the money notiert.
Berechnung des Delta
Die Berechnung des Deltas stimmt mit allen anderen Optionsgriechen überein. Die Berechnung erfolgt mit dem Black-Scholes-Modell. Dabei handelt es sich rechnerisch um die erste Ableitung der Black-Scholes-Formel basierend auf dem Kurs des Basiswerts. Da die Berechnung überaus komplex ist, erfolgt diese softwarebasiert. Die Broker bieten diese Berechnung an. Optionshändler können somit immer auf das aktuelle Delta zugreifen und dieses zur Bewertung von Optionen nutzen. Dabei referiert das Delta nur auf die Veränderung des Basiswerts. Andere Einflussfaktoren, die den Preis der Option verändern, werden nicht berücksichtigt.
Das Delta kommt häufig zum Einsatz, um abzuschätzen, wie viele Aktien durch eine Position von Optionen abgebildet werden können. Denn für diese Berechnung braucht man drei Faktoren:
- Anzahl der Optionen
- Größe des Kontrakts
- Kennzahl Delta
Deltaposition = Anzahl der Optionen x Kontraktgröße x Delta
Beispielsweise kauft ein Anleger 10 Optionen mit einer typischen Größe des Kontrakts von 100 Aktien. Das Delta könnte in diesem Beispiel bei 0,5 liegen. Dann würde die Deltaposition wie folgt berechnet:
10 x 100 x 0,5 = 500
Die Optionsposition spiegelt nun 500 Stücke des Basiswerts dar. Wenn sich der Kurs des Basiswerts dann um eine Geldeinheit verändert, ändert sich die Optionsposition um 350 Euro.
Tipp: Jetzt über 1.000 verschiedene Optionen zu besten Konditionen traden:
- In Deutschland Reguliert (BaFin)
- Sehr großes Angebot an Assets
- Viele Finanzprodukte
- Gutes Weiterbildungsangebot
- Schnelle Marktausführung
- Streng reguliert
- 24/7 Support
- Garantierte Stops möglich
- Nutzerfreundliche Plattform
- Große Auswahl an CFDs und echten Aktien
Delta und die anderen Optionsgriechen
Die Kennzahl Delta ist der zentrale Optionsgrieche. Viele Optionshändler erachten das Delta als die wichtigste Sensitivitätskennzahl. Im Zusammenhang mit dem Delta bedarf auch das Gamma Berücksichtigung, welches ausdrücklich die Veränderung des Deltas darstellt.

Diese wird in Relation zur Veränderung des Basiswerts berechnet. Als eine von mehreren Optionsgriechen ist das Delta von hoher Bedeutung. Optionshändler sollten jedoch die vier bekanntesten Sensitivitätskennzahlen allesamt beherrschen:
- Delta: Auswirkungen einer Kursänderung auf den Preis einer Option
- Gamma: Auswirkungen einer Kursänderung auf das Delta einer Option
- Theta: Auswirkungen des Zeitverlaufs auf den Preis einer Option
- Vega: Auswirkungen der impliziten Volatilität auf den Preis einer Option
Fazit: Die Bedeutung des Optionsgriechen Delta
Die Kennzahl Delta ist die wichtigste Kennzahl unter den Optionsgriechen. Damit kann das Delta die Preisänderung einer Option in Relation zur Kursänderung im Kurs des Basiswerts darstellen. Zugleich lässt sich mit dem Delta berechnen, welche Aktienanzahl in einer Optionsposition abgebildet wird, um mit der Deltaposition das eigene Portfolio zu hedgen. Die Kennzahl Delta bewegt sich dabei zwischen den Werten -1 und +1. Während eine Call Option ein positives Delta annehmen kann, ist es bei Put Optionen ein negatives Delta.
Mein Tipp: Jetzt über zahlreiche Optionen zu den besten Konditionen bei IG traden:
Meist gestellte Fragen:
Was sagt das Delta einer Option aus?
Das Delta einer Option gibt an, um wie viel sich die Optionsprämie ändert, wenn der Basiswert um 1 USD steigt oder fällt. Das Delta gibt somit Aufschluss über die Änderungsrate des Optionspreises bezogen auf den Kurs des Basiswerts.
Wann ändert sich das Delta einer Option?
Das Delta einer Option ändert sich ebenfalls, wenn sich der Kurs des Basiswertes verändert. Die Änderungsrate des Delta wird als Gamma bezeichnet.
Wo kann ich das Delta einer Option einsehen?
Jeder Broker, der den Handel mit Optionen erlaubt, sollte das Delta einer Option leicht auffindbar in seiner Handelsplattform anzeigen, wenn die entsprechende Option ausgewählt ist. Wo genau Sie das Delta finden, hängt aber von der jeweiligen Plattform ab.
Welchen Nutzen hat das Delta einer Option?
Am Delta lässt sich die Wahrscheinlichkeit ablesen, ob die Option bis zum Verfallstermin den Strike-Price erreicht. Je kleiner das Delta, umso niedriger die Wahrscheinlichkeit, dass die Option rechtzeitig zum Verfallstermin „im Geld“ sein wird.
Wie berechne ich das Delta einer Option?
Um das Delta einer Option zu berechnen, müssen Sie die sogenannte Black-Scholes Formel anwenden. Diese ist relativ kompliziert, allerdings wird das Delta bei fast allen gängigen Handelsplattformen automatisch berechnet und angezeigt, sodass Sie in der Regel nicht selbst nachrechnen müssen.