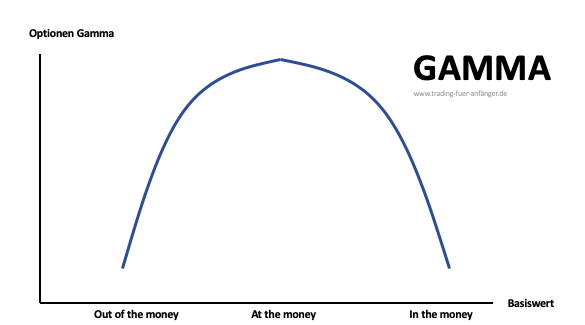
Beim Gamma Hedging handelt es sich um Strategie zur Absicherung. Optionshändler wollen die Auswirkungen bei starken Kursschwankungen des Basiswertes minimieren. Damit verfolgt man das Ziel, die primäre Strategie mit Optionen gegen eine starke Volatilität zu schützen. Im folgenden Beitrag geht es um Definition und Funktionsweise vom Gamma Hedging.
Gamma Hedging bei Optionen: Fakten in Kürze
- Gamma Hedging dient der Absicherung von Optionen.
- Die Strategie greift häufig am Tag der Fälligkeit einer Option.
- Sowohl Short als auch Long Calls können Teil der Strategie sein.
Definition vom Gamma Hedging
Das Gamma Hedging kommt zur Absicherung von Optionspositionen zum Einsatz. Diese Optionen sollen die Auswirkungen einer starken Volatilität beim zugrunde liegenden Basiswert reduzieren. Wenn sich der Aktienkurs vom Basiswert zu weit entfernt, werden die Chancen für den Händler kleiner, von dieser Kursentwicklung zu profitieren. Folglich verfolgen Optionshändler mit dem Gamma Hedging das primäre Ziel, die implementierte Strategie mit Optionen gegen eine starke Volatilität abzusichern.
Dabei spielt es keine Rolle, ob der Kurs nach oben oder nach unten abweicht. Das Gamma Hedging ist eine Strategie, die sich insbesondere für die Tage vor der Fälligkeit der Optionen eignet. Oftmals wollen Trader die Optionspositionen nur kurzfristig absichern.
Mein Tipp: Jetzt über zahlreiche Optionen zu den besten Konditionen bei IG traden:
Funktionsweise vom Gamma Hedging
Das Gamma Hedging kommt dann zum Einsatz, wenn bereits bestehende Optionspositionen vorhanden sind. Dann kaufen oder verkaufen die Optionshändler zusätzliche Kontrakte. Diese positionieren sich meist konträr zu den laufenden Optionen, die schließlich abgesichert werden sollen.
Wenn das Portfolio eines Optionshändlers verschiedene Long Calls enthält, kann der Optionshändler eine Put Option eröffnen, um die kurzfristigen Preisschwankungen (nach unten) zu kompensieren. Zugleich ist es möglich, Short Calls zu implementieren, die konträr zum Long Call stehen. Dabei wählen die Optionshändler einen abweichenden Strike im Vergleich zu den bereits vorhandenen Kontrakten.
Gamma & Delta einer Option
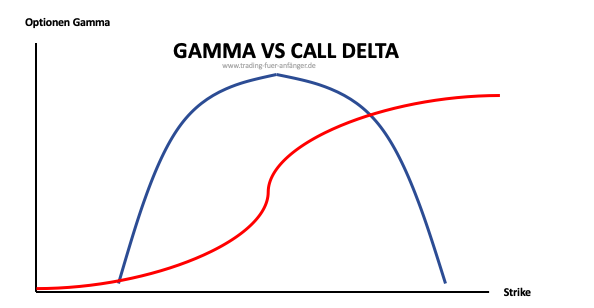
Beim Gamma und Delta handelt es sich um zwei Optionsgriechen. Diese Kennzahlen helfen den Optionshändlern bei der fundierten Beurteilung von Optionen. Beide Kennzahlen verfolgen das Ziel, den Zusammenhang der Preise der Optionen mit dem Kurs des jeweiligen Basiswerts nachzuvollziehen.
Die beiden Kennzahlen Gamma und Delta basieren hinsichtlich der Berechnung auf dem Black-Scholes-Modell. Mit diesem erfolgt die Berechnung der Optionspreise weltweit. Obgleich für eine präzise Berechnung der Preise einer Option diese Kennzahlen erforderlich sind, können die meisten Optionshändler diese nicht selbst ausführen. Dies ist jedoch nicht weiter schlimm.
Schließlich stellen Broker Softwarelösungen zur Verfügung, die die Berechnung der einzelnen Kennzahlen übernehmen. Dennoch sollten Trader die Optionsgriechen und deren Einfluss kennen, um die berechneten Werte zu interpretieren. Auf dessen Basis lässt sich dann die geeignete Optionsstrategie implementieren.
- Das Delta bildet dabei die Veränderung des Preises einer Option ab, wenn sich der Kurs des Basiswerts verändert. Optionshändler können somit immer genau sehen, wie sich die Veränderung um eine Preiseinheit beim Basiswert auf den Optionspreis auswirkt.
- Das Gamma bildet dabei den Zusammenhang vom Delta und der Preisveränderung ab. Hier geht es darum, wie stark sich das Delta einer Option verändert, wenn der Preis um eine Einheit nach oben oder unten abweicht. Wenn das Gamma Null beträgt, bleibt der Deltawert einer Option immer gleich.
Tipp: Jetzt über 1.000 verschiedene Optionen zu besten Konditionen traden:
- In Deutschland Reguliert (BaFin)
- Sehr großes Angebot an Assets
- Viele Finanzprodukte
- Gutes Weiterbildungsangebot
- Schnelle Marktausführung
- Streng reguliert
- 24/7 Support
- Garantierte Stops möglich
- Nutzerfreundliche Plattform
- Große Auswahl an CFDs und echten Aktien
Gamma Hedging vs. Delta Hedging
Wenn Optionshändler deltaneutrale Positionen erreichen wollen, gehen diese davon aus, dass kurzfristig starke Preisschwankungen einer implementierten Optionsstrategie schaden. Somit basieren das Delta und Gamma Hedging auf ähnlichen Annahmen. Dennoch kann das Delta Hedging nicht dazu führen, dass Optionshändler vollständig geschützt sind. Dies trifft insbesondere dann zu, wenn die Fälligkeit der Option in den nächsten Tagen bevorsteht. Denn dann bleibt so wenig Zeit, dass bereits eine normale Volatilität starke Veränderungen beim Preis einer Option verursacht. Um diesem Umstand gerecht zu werden, ergänzen Trader eine deltaneutrale Strategie mit dem Ansatz des Gamma Hedgings. Trader kaufen oder verkaufen Optionen auf den gleichen Basiswert, um den Gammawert zu reduzieren, sodass dieser im Anschluss Null beträgt. Damit möchte man sich vor starken Kursänderungen beim Basiswert schützen. Schließlich ist der Zeitwert kurz vor der Fälligkeit nur noch gering.
Das Delta Hedging lässt sich relativ unkompliziert umsetzen. Trader kaufen beispielsweise Call Optionen, um im gleichen Moment eine korrespondierende Anzahl an Teilen leer zu verkaufen. Wenn der Kurs des Basiswerts stagniert, obgleich die Volatilität anzieht, macht der Trader Gewinne. Allerdings minimiert der Zeitwertverlust diese Gewinne, da dieser exponentiell mit dem Verstreichen von Zeit ansteigt. Zusätzlich zur leerverkauften Position kann der Trader einen Short Call auf denselben Basiswert implementieren. Dabei wählt man einen abweichenden Strike im Vergleich zum Long Call. Mit diesem Ansatz lässt sich der Zeitwertverlust kompensieren, sodass die Veränderungen beim Delta geringer werden.
Fazit: Mit Gamma Hedging Positionen absichern
Das Gamma Hedging ist eine Strategie zur Absicherung einer Optionsposition, mit denen der Trader die Auswirkungen von einer starken Volatilität beim Basiswert reduzieren möchte. Diese Strategie eignet sich vornehmlich für erfahrene Optionshändler, da die Berechnung und Umsetzung relativ komplex ist. Zugleich ist eine kontinuierliche Beobachtung der Positionen erforderlich.
Beim Gamma Hedging werden zusätzliche Kontrakte zu den bereits vorhandenen Optionen verkauft oder gekauft. Damit positionieren sich die Trader gegensätzlich zu den Positionen, welche abgesichert werden sollen. Das Gamma Hedging eignet sich somit ideal, um die primär implementierte Strategie gegen starke Schwankungen im Kurs des Basiswerts abzusichern. Häufig kommt dieser Ansatz kurzfristig zum Einsatz – insbesondere in den Tagen vor der Fälligkeit der Optionskontrakte. Vielversprechend ist auch eine Kombination des Delta Hedges mit dem Gamma Hedging, die sich jedoch nur für sehr erfahrene Trader eignet.
Mein Tipp: Jetzt über zahlreiche Optionen zu den besten Konditionen bei IG traden:
