Bei der impliziten Volatilität handelt es sich um eine der wichtigsten Kennzahlen im Handel mit Optionen. Unter Berücksichtigung der impliziten Volatilität lassen sich Strategien und Entscheidungen ableiten, um die Erfolgschancen im Optionshandel zu erhöhen. Denn die implizite Volatilität gibt Aufschluss über die generelle Stimmung am Markt und die Erwartungen hinsichtlich der zukünftigen Entwicklung des Basiswerts. Da die Kenntnis der impliziten Volatilität und ihrer Eigenarten für den Optionshändler zwingend erforderlich ist, gibt es im folgenden Beitrag mehr Informationen.
Die implizite Volatilität einer Option erklärt:
- Die implizite Volatilität ist eine Kennzahl die Aussagen über die Zukunft ermöglicht.
- Sie gibt Auskunft über die zukünftig zu erwarteten Schwankungen der Wertpapierrenditen.
- Für strategische Herleitungen sind grundlegend Kenntnisse über Volatilität, Standardabweichung, Normalverteilung und Vega erforderlich.
Volatilität: Wofür steht sie?
In der Finanzwissenschaft erfährt die Volatilität große Berücksichtigung. Diese Kennzahl ist auch für das Handeln an den Finanzmärkten und somit auch für den Optionshandel wichtig. Denn die Volatilität hilft bei der Identifizierung des individuellen Risikos. Grundsätzlich wird die Volatilität in der Statistik mit der Standardabweichung dargestellt, die sich auf die jährliche Rendite einer Option bezieht. Folglich ist es für Trader wichtig, sowohl die Volatilität als auch die Standardabweichung zu verstehen, die auch regelmäßig synonym verwandt werden.
Mein Tipp: Jetzt über zahlreiche Optionen zu den besten Konditionen bei IG traden:
Die Standardabweichung
Bei der Standardabweichung handelt es sich um eine bestimmte Streuung, die auf die sog. Normalverteilung referiert. Beim Optionshandel und allgemein am Finanzmarkt muss jedoch berücksichtigt werden, dass die Renditen nicht vollständig der Normalverteilung unterliegen. Insbesondere bei der Betrachtung eines längeren Anlagezeitraums weichen die Renditen mitunter deutlich von dieser Normalverteilung ab. Die Standardabweichung ist in der Statistik die relevante Kennzahl, um die Streuung um einen Mittelwert auszudrücken. Damit lassen sich adäquate Aussagen zum vorhandenen Risiko treffen. Die Volatilität entspricht in diesem Sinne der Standardabweichung.
Normalverteilung
Die Standardabweichung und mithin die Volatilität sind nicht zu vernachlässigende Kennzahlen, die maßgeblich über den Erfolg im Optionshandel mitbestimmen. Um diese jedoch einwandfrei zu verstehen und erst recht zu interpretieren, müssen zumindest die Grundlagen der Normalverteilung beherrscht werden. Die Normalverteilung basiert auf folgenden Grundlagen:
- Eine Standardabweichung betrifft 68,27 % aller Messwerte. Diese liegen maximal eine Standardabweichung vom Durchschnitt als Mittelwert entfernt.
- Zwei Standardabweichungen betreffen 95,45 % aller Messwerte. Diese liegen maximal zwei Standardabweichungen vom Durchschnitt als Mittelwert entfernt.
- Drei Standardabweichungen betreffen 99,73 % aller Messwerte. Diese liegen maximal drei Standardabweichungen vom Durchschnitt als Mittelwert entfernt.
31,73 % aller Werte befinden sich mehr als eine Standardabweichung vom Durchschnitt entfernt. Daraus ergibt sich, dass nur etwas mehr als jede sechste Rendite schlechter als der Durchschnitt plus/minus eine Standardabweichung sein wird.
Die Arten der Volatilität
Grundsätzlich lassen sich zwei verschiedene Arten der Volatilität unterscheiden. Die historische und die implizite Volatilität. Beide Arten unterscheiden sich signifikant voneinander. Im folgenden Abschnitt werden beide Volatilitätsarten prägnant dargestellt.
Das ist die historische Volatilität
Die historische Volatilität referiert auf die vergangenheitsbezogenen Daten. Somit geht es um die historische Schwankungsbreite der Renditen. Hier ist immer ein bestimmtes Zeitintervall entscheidend.
Das ist die implizite Volatilität
Die implizite Volatilität bezieht sich demgegenüber auf die Zukunft. Hier geht es um die zukünftig erwarteten Schwankungen der Wertpapierrenditen. Diese können in ihrer Höhe von der historischen Volatilität abweichen. Die diesbezüglich abgebildete Volatilität korrespondiert mit der impliziten Volatilität. Die Berechnung und Ableitung erfolgt mit der Black-Scholes-Formel sowie dem sogenannten Iterationsverfahren.
Aussagekraft der impliziten Volatilität
Die implizite Volatilität gilt gemeinhin als eine der wichtigsten Kennzahlen im Optionshandel. Besonders bei der anfänglichen Entscheidung für eine bestimmte Strategie ist diese Kennzahl nicht zu unterschätzen. Doch was sagt die implizite Volatilität eigentlich aus? Im folgenden Abschnitt geht es um einige Kernelemente, die sich anhand dieser Kennzahl interpretieren lassen.
- Eine hohe implizite Volatilität führt regelmäßig zu einer höheren Schwankungsbreite als eine niedrigere implizite Volatilität.
- Die implizite Volatilität ist die erwartete Schwankungsbreite bei der Kursentwicklung des Basiswerts während der gesamten Laufzeit der Option.
Optionen mit einer geringeren impliziten Volatilität sind im Regelfall günstiger als Optionen mit einer höheren impliziten Volatilität. Doch Vorsicht – bei der Optionsprämie spielen noch andere Faktoren eine wichtige Rolle.
Tipp: Jetzt über 1.000 verschiedene Optionen zu besten Konditionen traden:
- In Deutschland Reguliert (BaFin)
- Sehr großes Angebot an Assets
- Viele Finanzprodukte
- Gutes Weiterbildungsangebot
- Schnelle Marktausführung
- Streng reguliert
- 24/7 Support
- Garantierte Stops möglich
- Nutzerfreundliche Plattform
- Große Auswahl an CFDs und echten Aktien
Kennzahl Vega
Griechische Buchstaben kommen im Optionshandel vielfältig zum Einsatz, um verschiedene Kennzahlen zu illustrieren. Mit dem griechischen Buchstaben Vega wird der Einfluss der impliziten Volatilität auf die Prämie der Option dargestellt. Andere Bezeichnungen für das Vega sind Kappa oder Lambda. Dies wird mit der ersten Ableitung der Optionsprämie nach der Volatilität ausgedrückt. Somit gibt die Kennzahl transparent an, wie sich die Prämie für eine Option in Beziehung zur veränderten Volatilität verhält. Wenn sich die implizite Volatilität um einen Prozentpunkt verändert, hat dies Auswirkungen auf den Optionspreis. Welche Auswirkungen genau, zeigt uns das Vega.
Die direkte Sensitivität der Volatilität lässt sich mit der folgenden Formel als Vega berechnen:
Vega (K/A) = Veränderung des Optionspreises (absolut) / Veränderung der impliziten Volatilität (absolut)
Der Anstieg der impliziten Volatilität verhält sich übrigens bei Call und Put Optionen dergestalt, dass die Preise für die Optionen ansteigen. Während bei vielen Kennzahlen Put und Call Option unterschiedlich oder sogar gegensätzlich reagieren, ist dies bei der impliziten Volatilität bzw. dem Vega nicht der Fall.
Der Volatilitätsindex
Die Volatilität am Finanzmarkt wird auch mithilfe verschiedener Indizes dargestellt. Der bekannteste Index ist der sogenannte VIX-Index (CBOE Volatility Index). Der VIX bildet die Erwartungen am Markt hinsichtlich der erwarteten Volatilität ab. Dabei bezieht sich die Berechnung auf die Optionspreise des S&P 500 Index. Die Berechnung erfolgt in Echtzeit. Allerdings gibt es eine Einschränkung bei der Berechnung dieses VIX-Index. Denn es werden nur die Optionen berücksichtigt, bei welchen der Fälligkeitstag an einem Freitag liegt und die Laufzeit zwischen 23 und 37 Tagen beträgt. Darauf basierend wird ein konstanter 30-Tage-Durchschnitt für die implizite Volatilität des Index ermittelt.
Die Aussagekraft des VIX-Index lässt sich wie folgt darstellen:
- Ein hoher Indexwert deutet auf eine volatile Marktphase hin, die von Unruhe und Unsicherheit geprägt ist.
- Ein niedriger Indexwert deutet auf eine Kursentwicklung hin, die ohne starke Schwankungen erfolgt.
Somit gibt es zwischen dem VIX Index und dem S&P 500 eine negative Korrelation. Der VIX Index ist als Indikator für die Einschätzung potentieller Risiken am Aktien- und Optionsmarkt von Bedeutung. Volatilitätsindizes existieren für die meisten bedeutenden Indizes.
Mein Tipp: Jetzt über zahlreiche Optionen zu den besten Konditionen bei IG traden:
Diese Strategien eignen sich für eine steigende implizite Volatilität
Verschiedene Strategien eignen sich dafür, um einen von einer anziehenden impliziten Volatilität zu profitieren. Dies ist mitunter ein dem Optionshandel immanenter Vorteil. Denn im Gegensatz zum physischen Besitz der Basiswerte kann man mit Optionen auch von Seitwärtsbewegungen oder einer erhöhten Volatilität profitieren.
Der Long Straddle ist eine neutrale Optionsstrategie, um von einer angestiegenen impliziten Volatilität zu profitieren. Hier geht der Trader von der Annahme aus, dass die Volatilität beim Basiswert in der nächsten Zeit steigt. Folglich kauft er gleichzeitig einen Put und einen Call, bei welchen Basiswert, Strike und Fälligkeit übereinstimmen. Durch den gleichzeitigen Kauf einer Long Position als Put und Call profitiert die Strategie von deutlichen Kursbewegungen sowie einem Anstieg der impliziten Volatilität. Denn dadurch steigt der Zeitwert der Option, woraus ein höherer Preis für die Option resultiert.
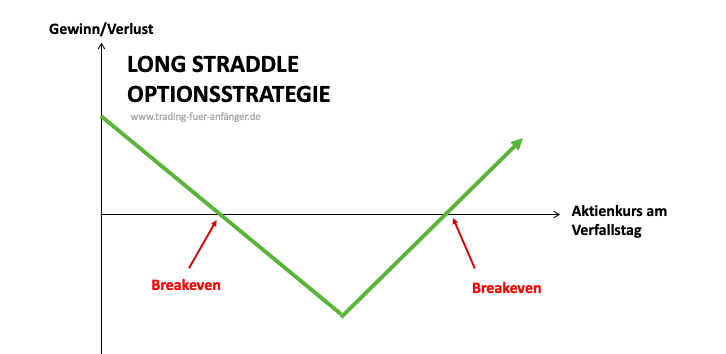
Diese Strategien eignen sich für eine sinkende implizite Volatilität
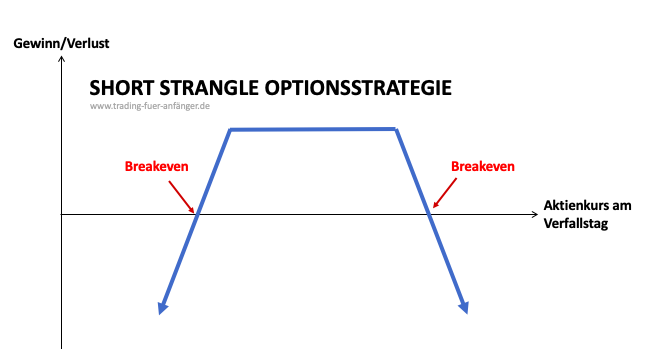
Umgekehrt können Trader auch von einer sinkenden impliziten Volatilität profitieren. Hierbei setzt man auf den Short Strangle als neutrale Handelsstrategie. Dabei hofft man auf eine Kursentwicklung, die innerhalb einer bestimmten Range verläuft. Der Trader verkauft gleichzeitig einen Put und einen Call. Die Strikes unterscheiden sich, während Basiswert und Laufzeit übereinstimmen. Die beiden Optionen sorgen dafür, dass die Position wertvoller wird, wenn sich die Kurse kaum bewegen und die implizite Volatilität abnimmt. Denn dadurch sinkt der Zeitwert der Optionen und zugleich der Optionspreis, da sich dieser aus Zeitwert und innerem Wert zusammensetzt.
Fazit: Die implizite Volatilität als Entscheidungsgröße
Optionshändler sollten die implizite Volatilität kennen, um die richtige Entscheidung für eine Optionsstrategie zu treffen. Dafür sind die hier dargestellten grundlegenden Kenntnisse über Volatilität, Standardabweichung, Normalverteilung und Vega erforderlich. Unter Berücksichtigung dieses Wissens lässt sich die ideale Strategie identifizieren, mit welcher Trader von einer erhöhten oder gesunkenen impliziten Volatilität profitieren.
Mein Tipp: Jetzt über zahlreiche Optionen zu den besten Konditionen bei IG traden:
